Uncertainty Analysis

This page will familiarize you with commonly used methods to estimate the accuracy of experimental data and quantities derived from this data.

Errors in experimental data consist of two components:

• Fixed or Systematic errors - cause repeated readings to be in error by a similar amount e.g. improperly calibrated or installed equipment.
• Random errors - caused by electronic fluctuations, friction etc.

The following technique for estimating the propagation of errors/uncertainties into the result is that proposed by Kline and Mclintock. We use specified uncertainties for primary experimental measurements e.g. p = 500Pa ± 10Pa, where ±10Pa is the uncertainty.

Method

Take measurements with estimated uncertainty for each measurement. Then estimate the uncertainty in the result R as a function of independent variables xi. Thus

R=R(x₁,x₂,..,x_n)

Let wR be the uncertainty in the result and wi the uncertainty in the independent variables. Then the uncertainty in the result is

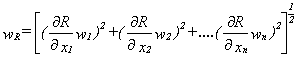
Example:

The speed indicated by a Pitot static tube is given by:

where Δp is the dynamic pressure indicated by the Pitot tube and r is the gas density at the measurement point. Thus the uncertainty in the speed may be estimated as:

As an example, assume the measured independent values and their estimated uncertainties are:

Δp=600Pa ± 0.5%

ρ=1.18kg/m³ ± 0.03 kg/m³

Estimate the uncertainty in the speed w_v

∂v/∂Δp = 0.5(2/ρΔp)^0.5

∂v/∂ρ = -0.5(2Δp)^0.5/ρ^1.5

thus the uncertainty in the speed w_v is:

w_v = 0.413m/s

and

w_v / v = 0.413 / 31.89 = 1.29%

How do we estimate the uncertainty?

1) By repeating experimental readings. Then estimate uncertainty within a certain confidence interval. Pertains to random errors as for a sufficient number of readings random errors tend to approach a Gaussian distribution allowing statistical analysis.

2) Experience.

Expanding on point 1), suppose we have repeated a set readings. Let n be the number of readings and xi a particular reading.

then the arithmetic mean is given by

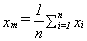
the deviation from the mean for each reading is given by

d_i = x_i-x_m

the average of the absolute value of the deviations is given by

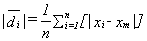
and the root mean square deviation or standard deviation is given by

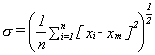
for a large number of readings or

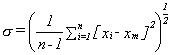
for a small data set (n < 20)

From statistical analysis define

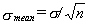
Then the uncertainties are

• σ_mean for a 68.3% probability
• 2σ_mean for a 95.5% probability
• 3σ_mean for a 99.7% probability

Thus the repeated data may be expressed as

• x_m ± σ_mean for a 68.3% probability (i.e. there is a 68.3% probability that the measurement will lie within ± σ_mean etc)
• x_m ± 2σ_mean for a 95.5% probability
• x_m ± 3σ_mean for a 99.7% probability